
Typically, the more distant fiber(s) are of interest. Where I_x the moment of inertia of the section around x axis and Y the distance from centroid, of a section fiber, parallel to the x axis and measured perpendicularly from it. The elastic modulus S_x of any cross section around axis x (centroidal), describes the response of the section under elastic flexural bending. Where the I_x and I_y are the moments of inertia around axes x and y, which are mutually perpendicular with z and meet at a common origin. The calculation of the polar moment of inertia I_z around an axis z (that is perpendicular to the section plane), can be done with the Perpendicular Axes Theorem: The polar moment of inertia, describes the rigidity of a cross-section against torsional moments, likewise the planar moments of inertia, described above, are related to flexural bending. The dimensions of moment of inertia are ^4.

Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the resulting curvature is reversely proportional to the moment of inertia I. Where E is the Young's modulus, a property of the material, and \kappa the curvature of the beam due to the applied load. The bending moment M, applied to a cross-section, is related with its moment of inertia with the following equation: The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. This entry was posted in Introductory Problems, Volumes by cross-section on Jby mh225.The area A and the perimeter P of a rectangular cross-section, with sides b and h, can be found with the next formulas: The cross-sections are circles of radius x 2, so the cross-sectional area is A(x) π⋅(x 2) 2π⋅x 4 The volume is V = ∫ -1 1A(x) dx = ∫ -1 1 π⋅x 4 dx = π⋅(x 5/5)| -1 1 = 2π/5

Find the volume of the solid obtained by rotating the curve y = x 2, -1 ≤ x ≤ 1, about the x-axis. where x⋅ex 2 was integrated using the substitution u = x 2, so du = 2xdx.ĥ. The area is A(x) = base ⋅ height = x⋅ex 2. Find the volume of the solid with cross-section a rectangle of base x and height e x 2 Answerġ. where cos(x)sin 2(x) is integrated using the substitution u = sin(x), so du = cos(x) dx.Ĥ. Find the volume of the solid with circular cross-section of radius cos 3/2(x), for 0 ≤ x ≤ π/2. Recall an ellipse with semi-major axis a and semi-minor axis b has area πab, so this ellipse with semi-major axis x 2 and semi-minor axis x 3 has the area: A(x) = π⋅x 2⋅x 3 = π⋅x 5.
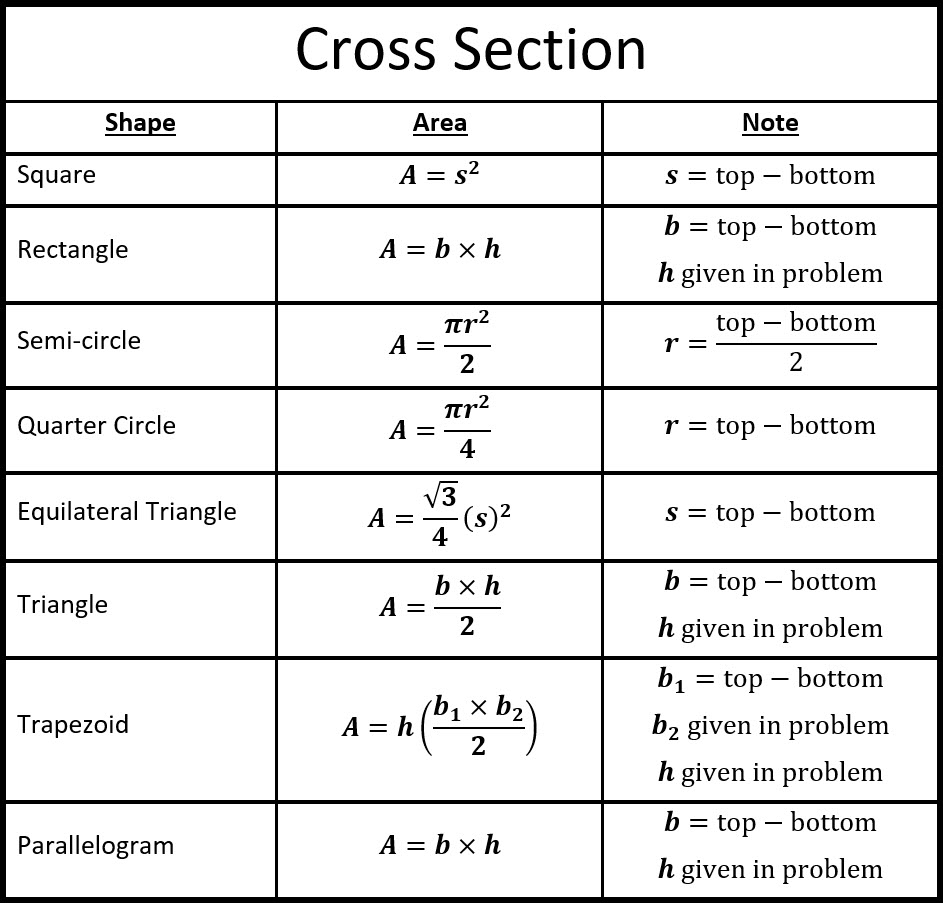
Find the volume if the solid with elliptical cross-section perpendicular to the x-axis, with semi-major axis x 2 and semi-minor axis x 3, for 0 ≤ x ≤ 1 Answerġ.

Find the volume of the solid with right isosceles triangular cross-section perpendicular to the x-axis, with base x 2, for 0 ≤ x ≤ 1 Answerġ.


 0 kommentar(er)
0 kommentar(er)
